It is common for physics grad students to remember the angular momentum operator

. Many will even remember that it commutes with

and we can therefore form a set of simultaneous eigenfunctions to describe a particle in angular momentum space. Some may even recall that the standard conventions yield the following eigenequations.
But do you know how to demonstrate that
)
and
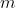
are the eigenvalues for

and

?
for Stache: 
) and
and 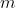 are the eigenvalues for
are the eigenvalues for  and
and  ?
?
I must know nothing. I thought that m was the eigenvalue of Lz by definition. But in my memory, the eigenvalue of L squared follows from the commutation relations. Right?
ReplyDeleteYou can of course always renormalize the quantum numbers to make one of them whatever you wish. However you still must show that m ranges from -j to j and moves in integer steps. Of course you begin with J_z|j,m> = \mu |j,m> and J^2|j,m>=\lambda|j,m>. Then later you relate \lambda to \mu and then decide to take \mu = m which in turn forces \lambda = j(j+1)
ReplyDelete