The standard model tells us that all particles of the same type are indistinguishable. Therefore when describing a system of multiple particles (of the same time) we must take great care to insure our particles are treated as indistinguishable. Accidentally treating particles as identical can cause serious miscalculations. For example (not physics but very illustrative):
For the following questions assume I have two children, child A and child B: the probability of any individual child being a boy is 1/2, the probability of the child being born on a Tuesday is 1/7, etc. For each question I will apply a different set of constraints. Only the constraints mentioned in the question affect that question.
Q1: What is the probability I have two boys?
A1: 1/4.
Q2: Child A is a boy. What is the probability I have two boys?
A2: 1/2.
Q3: At least one of my children is a boy. What is the probability I have two boys?
A3: 1/3.
Q4: At least one of my children is a boy born on Tuesday. What is the probability I have two boys?
A4: 13/27.
The reason for the counterintuitive answers to questions 3 and 4 is that we don't know which child (A or B) satisfies the constraint. Since it could be either the probability of overlap changes the result. The more (less) probable the overlap the closer the answer is to 1/3 (1/2).
But what does this have to do with particle decay?
Quantum Mechanics says there are no hidden variables. If the time a particle had been "alive" affected the probability it would decay in the future then there would have to be some hidden variable to fully describe the particle! If we could look at a particle and tell how long it had been alive then particles would not be indistinguishable!
) and
and 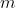 are the eigenvalues for
are the eigenvalues for  and
and  ?
?

